机器学习中分类问题中的性能指标
1. TP / FP / FN / TN
| 预测 1 | 预测 0 | |
|---|---|---|
| 实际 1 | True Positive (TP) | False Negative (FN) |
| 实际 0 | False Positive (FP) | True Negative (TN) |
2. 准确率 (Accuracy)
- 定义:预测正确的样例占所有样例的比例。
- Accuracy = (TP + TN) / (TP + FN + FP + TN)
- 存在问题:一个地震的分类器,0 表示没有地震,1 表示地震,由于地震概率非常小,因此,只要所有的例子来都猜是 0,就能够是准确率 (Accuracy) 达到 0.9999,但我们更关心的是发生的概率。
3. 精确率 (Precision)
- 定义:精确率又叫查准率,是在所有被判断为正样例的样本中真正是正样例的比例。
- Precision = TP / (TP + FP)
- 用途:精确率常用于推荐系统中。对某个商品,用户喜欢为正样例,不喜欢为负样例,以精确率来衡量推荐的性能。
4. 召回率 (Recall)
- 定义:也被成为查全率,医学上也被称为敏感度(Sensitive),正样本被预测出的概率。
- Recall = TP / (TP + FN)
- 用途:如医学中需避免漏诊,需用召回率评价。
5. 特异度 (Specificity)
- 定义:负样本被检测出的概率。
- Specificity = TN / (FN + TN)
- 用途:也常用于医学,如果特异度极低,那则考虑为误诊率极高。
6. ROC 曲线
- 定义:Receiver Operating Characteristic, ROC,曲线上每个点反映着对同一信号刺激的感受性。
- 横轴 :假正类率(False Positive Rate, FPR),1 – 特异度,即 1 – Specificity。可以认为是代价(理解为上文中提到的 误诊率)。
- 纵轴:真正类率(True Positive Rate, TPR),灵敏度,Sensitivity。可以认为是收益。(理解为上文中提到的某病患被检测出的概率)。
- 变量:二分类中的阈值。
- 例:某二分类问题
| 阈值(%) | 实例数 | 正例数 | 1 – 特异度(%) | 敏感度(%) |
|---|---|---|---|---|
| 10 | 6180 | 4879 | 2.73 | 34.64 |
| 20 | 6180 | 2804 | 9.80 | 54.55 |
| 30 | 6180 | 2165 | 18.22 | 69.92 |
| 40 | 6180 | 1506 | 28.01 | 80.62 |
| 50 | 6180 | 987 | 38.90 | 87.62 |
| 60 | 6180 | 529 | 50.74 | 91.38 |
| 70 | 6180 | 365 | 62.93 | 93.97 |
| 80 | 6180 | 294 | 75.26 | 96.06 |
| 90 | 6180 | 297 | 87.59 | 98.17 |
| 100 | 6180 | 258 | 100.00 | 100.00 |
ROC 曲线:
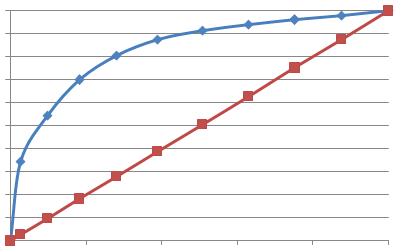
- 评价 :我们希望,在 误诊率 最小的情况下达到查出 尽可能所有的病患 ,当 ROC 曲线约靠近(0, 1) 点时,也就是 ROC 曲线下的面积越大时,分类器的性能越好。
7. AUC
- 定义:Area Under curve, AUC。ROC 曲线下的面积。
- 评价:越大认为分类器性能越好,同 6 中所描述。
8. F1 score
- 定义:精确率和召回率的调和平均数。
- F1 = 2 / [(1 / Pre) + (1 / Re)]
- 评价:F1 score 越高,认为分类器性能越好。
正文完